Embarking on a mathematical odyssey, we delve into the sine definition, an indispensable concept that permeates the realms of trigonometry and beyond. Its formula, domain, and range lay the groundwork for understanding this fundamental function.
Unraveling the sine function’s properties, we uncover its periodicity, amplitude, and symmetry, illustrated through captivating examples. Its practical applications span diverse fields, from physics to engineering, demonstrating its versatility in modeling real-world phenomena.
Sine Function Definition
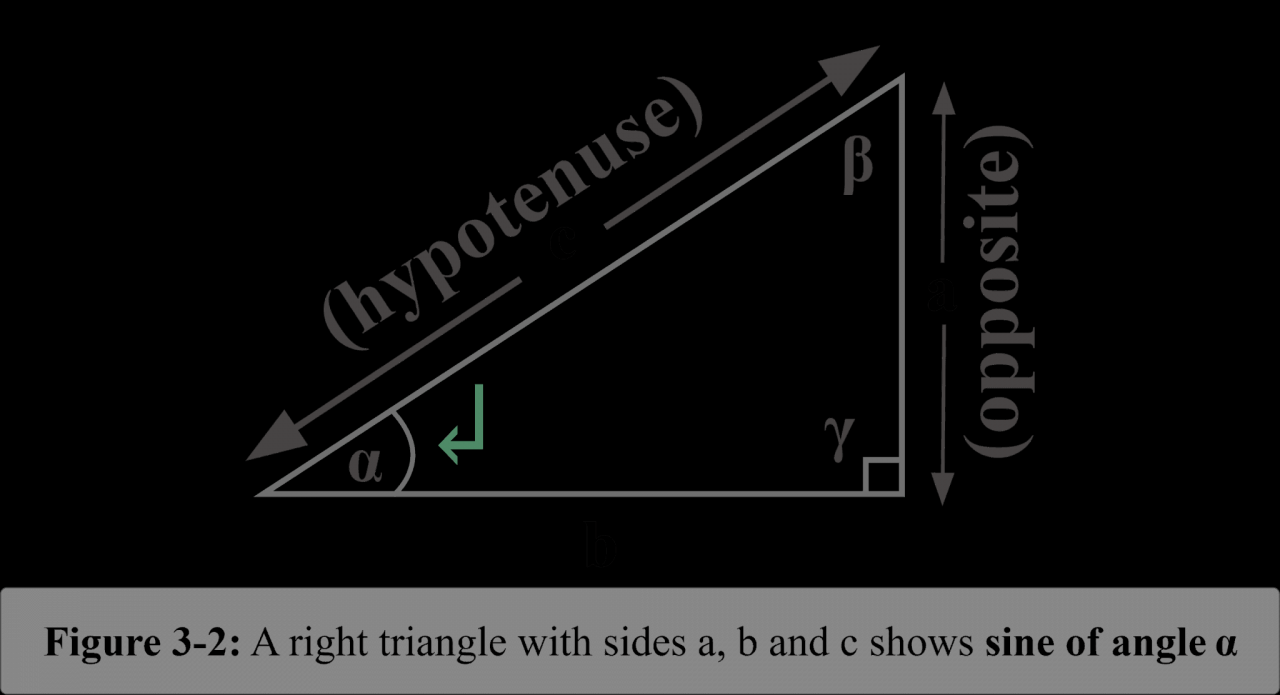
The sine function is a mathematical function that describes the vertical component of a point moving in a circular motion. It is defined as the ratio of the length of the opposite side to the length of the hypotenuse of a right triangle with an angle equal to the input angle.
The formula for the sine function is:
sin(θ) = opposite / hypotenuse
where θ is the angle in radians.
The domain of the sine function is all real numbers, and the range is -1 to 1.
Properties of the Sine Function, Sine definition
- Periodicity:The sine function is periodic with a period of 2π, meaning that it repeats itself every 2π radians.
- Amplitude:The amplitude of the sine function is 1, meaning that it oscillates between -1 and 1.
- Symmetry:The sine function is an odd function, meaning that it is symmetric about the origin.
Applications of the Sine Function
The sine function has a wide range of applications in various fields, including:
- Physics:The sine function is used to describe the motion of objects in circular motion, such as the motion of a pendulum or a planet orbiting the sun.
- Engineering:The sine function is used to design and analyze structures that are subjected to periodic forces, such as bridges and buildings.
- Signal processing:The sine function is used to analyze and process signals, such as audio and video signals.
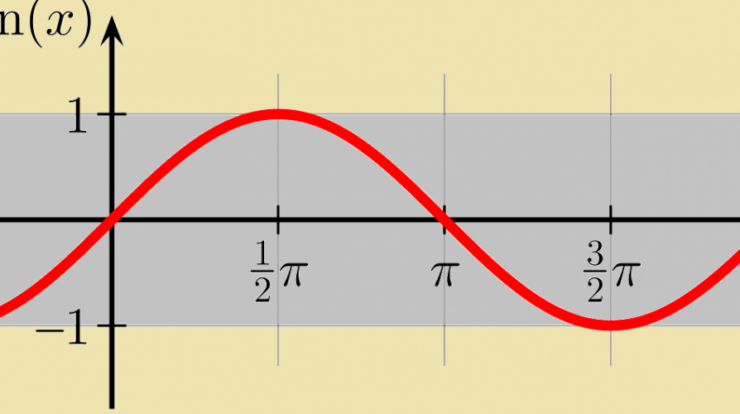
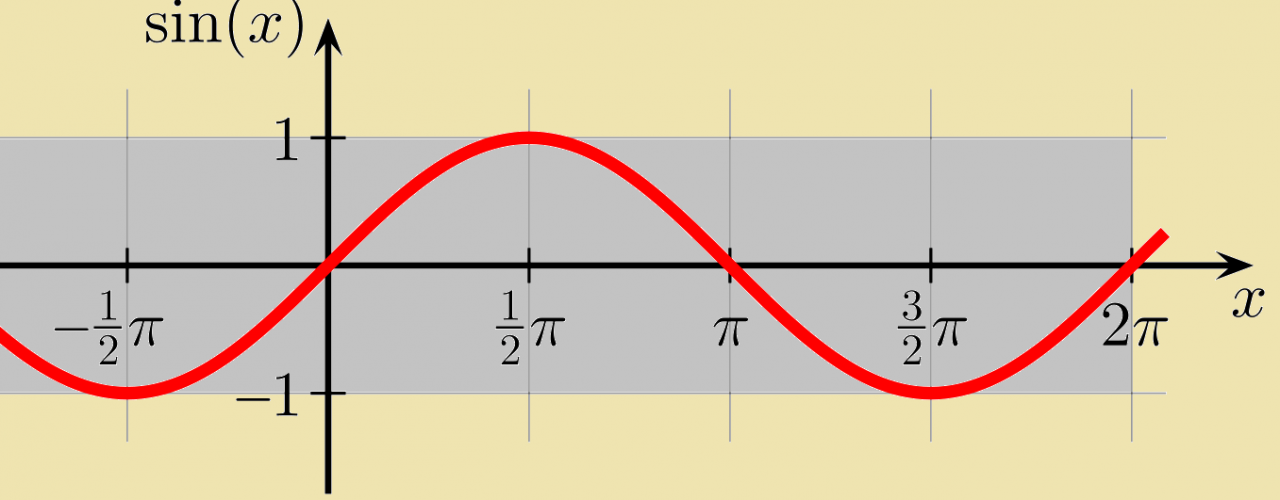
Graphical Representation of the Sine Function
The graph of the sine function is a wave that oscillates between -1 and 1.
| Angle (radians) | Sine |
|---|---|
| 0 | 0 |
| π/2 | 1 |
| π | 0 |
| 3π/2 | -1 |
| 2π | 0 |
Derivatives and Integrals of the Sine Function
The derivative of the sine function is the cosine function:
d/dx sin(x) = cos(x)
The integral of the sine function is the negative cosine function:
∫ sin(x) dx =
cos(x) + C
Inverse Sine Function
The inverse sine function, also known as the arcsine function, is the function that gives the angle whose sine is a given value.
The formula for the inverse sine function is:
sin-1(x) = θ
where -1 ≤ x ≤ 1 and -π/2 ≤ θ ≤ π/2.
Closure
As we conclude our exploration, the sine function emerges as a cornerstone of mathematical analysis, with its derivatives and integrals serving as powerful tools. The inverse sine function, or arcsine, completes the picture, providing a deeper understanding of trigonometric relationships.
General Inquiries: Sine Definition
What is the sine function?
The sine function is a trigonometric function that measures the vertical coordinate of a point on a unit circle corresponding to a given angle.
What is the formula for the sine function?
The formula for the sine function is sin(x) = y/r, where x is the angle, y is the vertical coordinate of the point on the unit circle, and r is the radius of the unit circle.
What is the domain and range of the sine function?
The domain of the sine function is all real numbers, and the range is [-1, 1].